簡単な小学生の計算問題（2021/06/02）

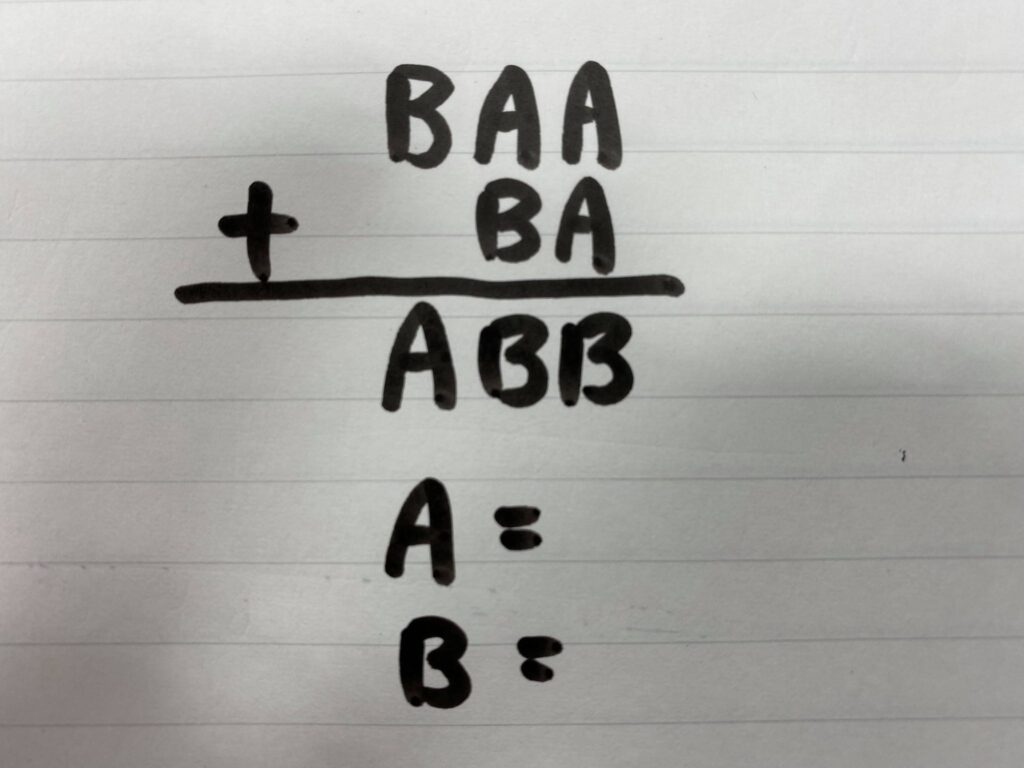
小学校5年生の算数の問題です（数学ではない）

写真は、小学校5年生の算数の問題だそうです。ラージAとラージBに入るアラビア数字をそれぞれ求めよという問題であり、厳密にAとBの値は数学的には違うのかもしれまえんが、良い問題だと思いました。

まず、小学校ですから、一桁の数字といえば0から9までの10種類ということになり、かつ、2つの数字を足しているので、合計値のほうが足されるそれぞれの数字より大きいのは自明です。ですので、A＞Bとなるでしょう。そうして、Aに一番大きい数字の9、Bに8を当てはめてみると、899+89=988でああ合っている、ということで解けました。

追記

より厳密には、
【一桁目】
A+A=10+B

【二桁目】
A+B+1=10+B
A+1=10
すなわちA=9

【三桁目】
A=B+1
すなわち
B=8

となります。

繰り上がりで溢れた数字を一桁上に加える、という技を駆使するには、AもBもできるだけ大きな数字にしたほうがいいだろうというふうにピンとくるのは数字のセンスです。実は、筆者にはそのセンスがありませんので、Aが2でBが1だったらどうだろうかとか考えて、全く合計値が不足するという失態を犯しながらとても時間がかかったわけなのですが、このような、数学的センスに代表される知力というものは、かなりの程度、訓練で身につくものです。天才的な数学者などが世の中にはいますが、こうした方々は、四六時中数学なら数学のことを無意識のレベルで考えているものであり、集中力が続く限り、机に向かったり思索したりするのが大好きな方々なのです。ですので、根本的に頭の出来が違うというわけではなくて、いかに、自分という貴重な人間リソースを、こうした自分が好きで向いている分野に振り向けて突き詰めることができるかによって人生は大きく変わるのではないかと考えています。

知力より大切なのは体力

学習といっても、身体が資本であることは当然でありまして、日本の歴史に燦然と輝く知の巨人であった、例えば弘法大師空海とか吉田松陰先生とかいった方々は、頭もズバ抜けていましたが同様に鬼の体力と頑健さを持ち合わせておりました。弘法大師空海が開山した人間の根本修行道場である高野山の麓に九度山という地名の集落がありますが、ここは、空海の母が麓にやってきた時、母親好きの空海は、なんとこの麓の村まで月に9回も降りてきて母親に会いに来た、という故事から九度山という地名になっているのです。九度山から高野山には、細く険しい山道で片道20キロメートル、こんな険しい往復40キロメートルの道を、月に9度も限界まで忙しい空海が、いかに修行の一環だといってもやってくるとは凄すぎます。そもそもこの人、現代人が月へ行くより遠かった、唐の長安に遣唐使で行って、20年の修行時間を2年に短縮し、当時の世界最強国であった唐で帝師と崇められていた恵果阿闍梨（けいかあじゃり）より、真言密教の全てを授けられるのです。恵果阿闍梨は空海と初めて顔を合わせた時、「やっと来たか。わたしはお前が来るのをずっと待っていた」と言ったそうです。毛外の蛮国からやってきた若者に、その奥義の全てを授けるとは、恵果阿闍梨も凄いですが空海とは精神的にも肉体的にも、とてつもない大きな存在だったと思うのです。

ことを為すにはまず体力が大切だというお話でした。

俺たちの松陰先生

さて、俺たちの吉田松陰先生、日米和親条約が締結され、ポーハタン号の船上で祝賀の宴が行われたその夜に、どうしてか海岸につないであった漁民の小舟を盗んで下田港内の小島から旗艦ポーハタン号に漕ぎ寄せ、乗りこみアメリカまで連れて行け、と談判するという離れ業（＊死罪相当です）を演じた俺たちの松陰先生についてのお話はまた今度にします。それでは本日も良い一日を。