素数
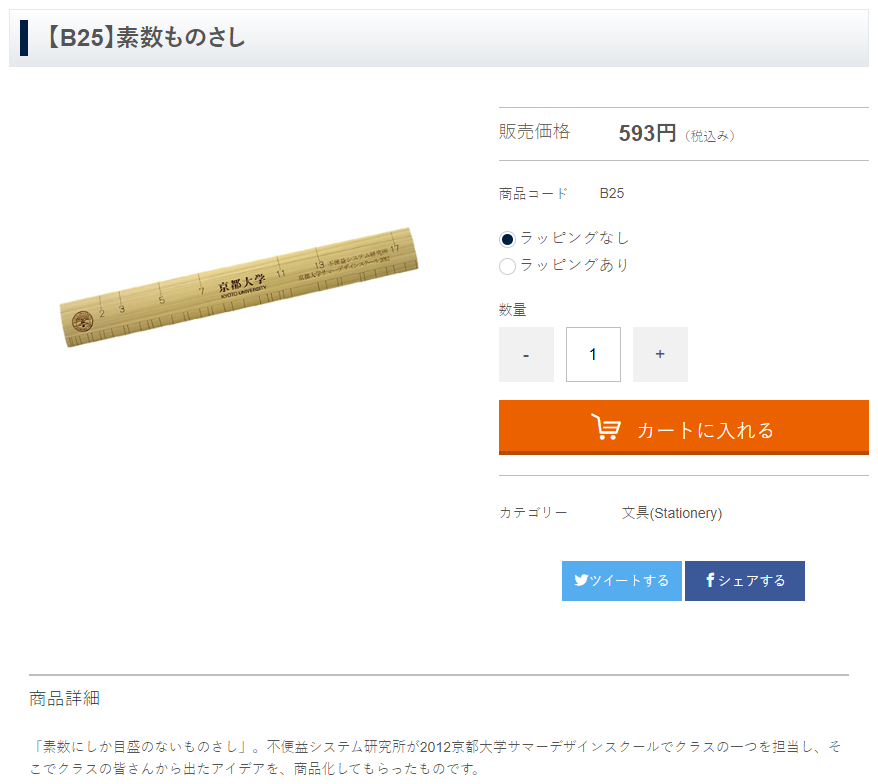
素数ものさし
素数が大好きな私のおすすめステーショナリーです。
最近この手の記事を暇なのか多くの人が読んでいるようで、面映ゆいところですが、無理せず、学習や早起きと同じく「今日だけ」の精神でやっていこうと思います。
さて、これは、素数ものさし、といって不便益システム研究所(京都大学)が世に出した、素数にしか目盛りのないものさしです。確かに、素数以外のすべての合成数は、素数の組み合わせでできていますから、究極的には、素数にだけ目盛りがあればすべての数を出すことができます。ただし、4を出すには13から17の間を測ればいいけどいろいろと面倒なところは確かにございます。6とか、けっこう難しいです。8とか9も。
素数とは
素数とは、1と自分自身以外の約数を持たない自然数です。つまり、他の数で割り切れない特別な数字なのです。例えば、2、3、5、7、11などが素数です。一方、4や6のように他の数でも割り切れる数は「合成数」と呼ばれます。「1」は素数なのでしょうか?「1」は素数ではありません。「1」を素数に含んでしまうという間違いがよく発生します。上で説明している「1と自分自身以外の約数を持たない自然数」という条件を「約数を2つしか持たない自然数」と置き換えて考えてみると、「1」は約数が1の1つしかないためこの条件に当てはまりませんね。つまり「1」は素数ではないということになります。素数の基本性質として、以下の特徴があります。
<無限性>
素数は無限に存在します。つまり、どんなに大きな自然数を考えても、新たな素数が必ず見つかるということです。
<唯一性>
素数は、それ自体と1を除いて他の素因数を持ちません。例えば、15の素因数は3と5ですが、それぞれは素数です。このように、合成数は素因数分解によって素数の積として表すことができます。
このブログに隠された素数
筆者は素数が大好きですから、このブログにも、素数を忍ばせています。つまり、ホームページに飛ぶとすぐ見える、直近24時間で読まれた23記事というコーナーの23は、当然素数です。続いて、更新した19記事、の19も素数ですし、週間上位29記事の29、月間上位31記事の31ももちろん素数です。最後に、通算閲覧上位97記事、の97ですが、これは100までの素数で最も大きい素数で、日本では、中学生までに誰でも学ぶことができます。
以上、素数のお話でした。
割り切れない思いを抱えて生きるのも、良いものです。
素数とか、唯一のものには名前がないとか、そんな記事ばっかり書いている筆者の息抜きは以上です。